O lançamento oblíquo é um dos problemas mais interessantes da cinemática, e nós vamos utilizar o sensor de velocidade do post anterior para estudar o lançamento oblíquo utilizando uma pista e carrinhos Hotwheels.
O salto do Hotwheels como um lançamento oblíquo
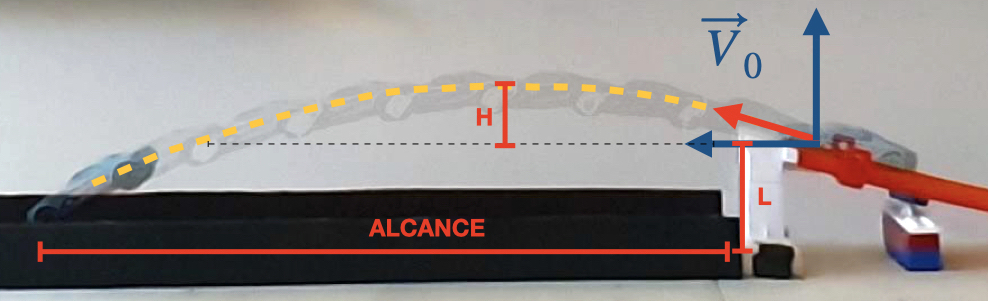
A Figura 1 mostra uma composição de fotos com a trajetória que o carrinho faz durante um salto. A trajetória lembra a um lançamento oblíquo que estudamos na escola, mas note que o ponto de lançamento está a uma altura $L$ acima do nível onde ele cai.
Agora veja como é legal o salto em câmera lenta!
Para estudar a física deste salto, utilizei uma pista Hotwheels composta por um lançador que põe o carrinho em movimento, uma rampa e uma caixa de areia para amortecer e marcar o ponto queda (como no salto a distância do atletismo), mostrada na Figura 2.

Quando acionamos o lançador, o carrinho é colocado em movimento com uma velocidade que depende da força com que batemos no lançador. O carrinho sobe a rampa, e realiza o salto. Se a a física estiver correta, o alcance do salto depende apenas do ângulo da rampa, da altura da rampa, e da velocidade com que o carrinho é lançado pela rampa.
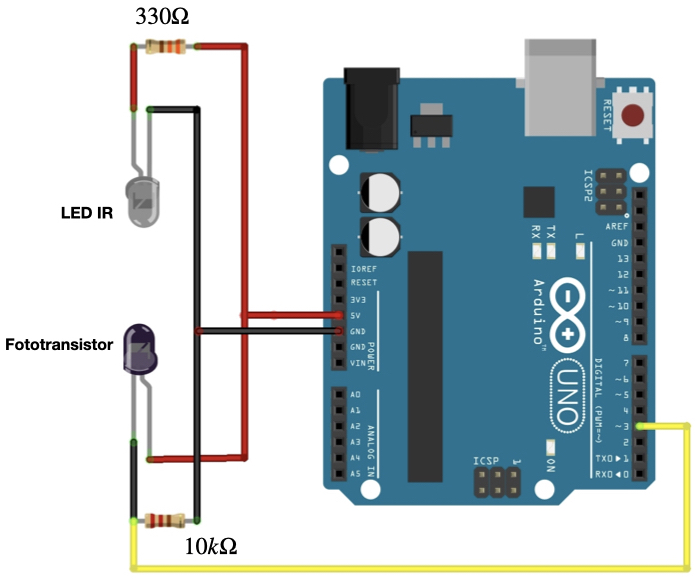
A angulação foi determinada com ajuda de uma régua, e a velocidade de lançamento pode ser medida adaptando-se o sensor de passagem na rampa. Tudo o que precisamos e saber o tamanho do carro e o tempo de passagem do carro pelo sensor com ajuda do Arduino, conforme mostrado no post anterior.
A física do lançamento oblíquo
O lançamento oblíquo consiste em corpo lançado com uma velocidade $V_0$ fazendo um ângulo $\theta$ com a horizontal, conforme mostrado na Figura 3.
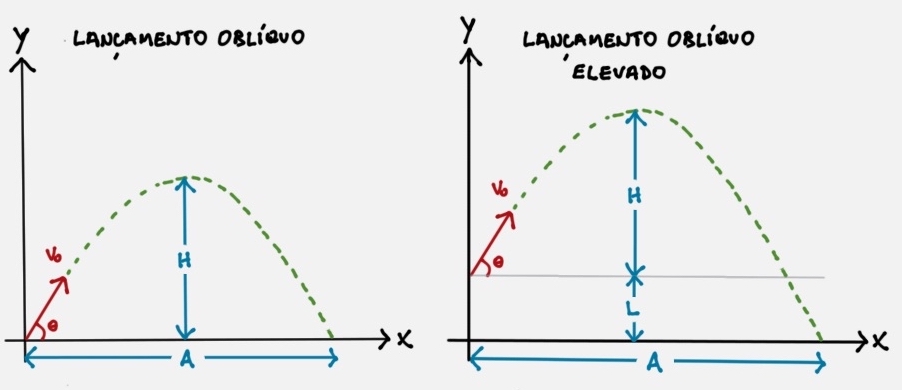
Se, após o lançamento a gravidade for a única força atuando no corpo (nenhum efeito da resistência do ar), o corpo realiza um MRU (movimento retilíneo uniforme) na direção horizontal, e um MRUV (movimento retilíneo uniformemente variado) na direção vertical. As coordenadas $x(t)$ e $y(t)$ do corpo são dadas por:
$$x(t) = x_0 + V_{0x} t$$
$$y(t) = y_0 + V_{0y} t – \frac{g}{2}t^2$$
onde $(x_0,y_0)$ é a posição inicial do corpo, $V_{0x} = V_0 \cos \theta$ e $V_{0y} = V_0 \sin \theta$, e $g$ é a aceleração da gravidade. Este conjunto de equações descreve uma trajetória parabólica com uma altura máxima de
$$H = \frac{\sin^2\theta}{2 g}V_0^2$$
e um alcance dado por
$$A = \frac{\sin 2\theta}{g}V_0^2$$
O lançamento oblíquo com elevação
No salto do Hotwheels, o carrinho obedece um lançamento oblíquo com elevação. O alcance deste salto é determinado por:
$$A = V_{0x}(t_s+t_d)$$
Onde $t_s$ é o tempo de subida, e $t_d$ o tempo de descida. Estes tempos podem ser facilmente calculados tirando-se vantagem do fato de que o corpo realiza um MRUV na direção vertical.
$$t_s = \frac{V_{oy}}{g}$$
$$t_d=\sqrt{\frac{2(H+L)}{g}}$$
Para encontrar uma expressão bonitinha para o alcance tem um pequeno truque matemático. No nosso experimento, sabemos qual é a altura $L$ da rampa, mas não sabemos em princípio qual a altura $H$, pois não temos como medí-la neste experimento. E isso impede que a gente determine $t_d$ com precisão. Mas a gente assume que $L<H$ (também não é garantido), de forma que obtemos:
$$t_d = \sqrt{\frac{2H}{g}\left(1+\frac{L}{H}\right)}$$
$$t_d = \sqrt{\frac{2H}{g}}\sqrt{1+\frac{L}{H}}\approx \frac{V_{0y}}{g}+\frac{L}{V_{0y}}$$
Para obter a expressão de $t_d$ acima, usamos a famosa expansão de Taylor $(1+x)^n \approx 1 + n x$ (valido apenas se $|x| < 1$), onde $n=1/2$ e $x = L/H$. Com os valores de $t_s$ e $t_d$ acima, finalmente encontramos que a altura máxima e o alcance do salto são dados por:
$$H= \frac{sin^2\theta}{2 g}V_{0}^2+L$$
$$A \approx \frac{\sin 2\theta}{g}V_{0}^2+\frac{L}{\tan \theta}$$
Note que a expressão do alcance se assemelha a uma função do tipo $y = b x + c$, onde $y = A$, $b = \sin 2\theta/g$, $x = V_0^2$ e $c = L/\tan \theta$. Note também que o alcance independe do comprimento e da massa dos carrinhos Hotwheels. Portanto, os resultados devem ser idêntico para carrinhos diferentes.
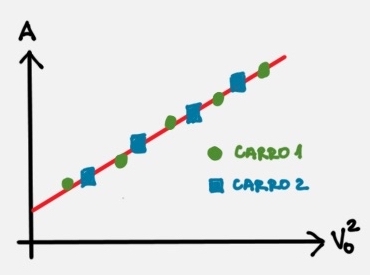
Se a teoria acima estiver correta, ao medirmos $A$ e $V_0$ de vários lançamentos de carrinhos diferentes e construirmos um gráfico de $A$ vs $V_0^2$, devemos obter um gráfico semelhante ao da Figura 4.
O experimento
Eu fiz uma série de experimentos com dois carrinhos diferentes, que foram lançados várias vezes cada um, com diferentes velocidades. Os dados obtidos são mostrados na Figura 5.
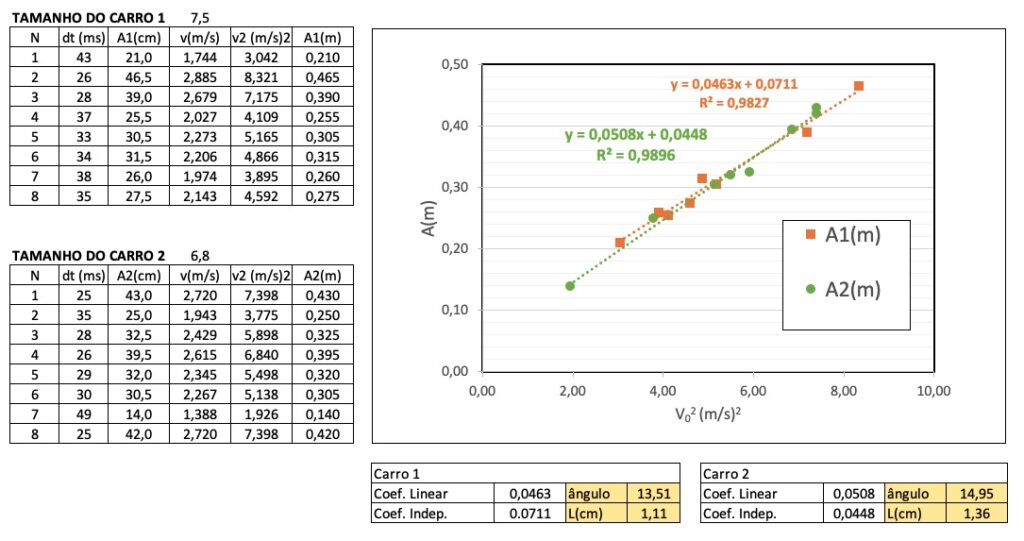
A Figura 5 mostra os dados medidos para 2 carros Hotwheels com diferentes tamanhos e pesos. Como não tenho controle da velocidade, os lançamentos não possuem nenhum ordem específica. Os saltos do carro 1 são indicados por quadrados laranja, e os saltos do carro 2 por círculos verde. Os dados de cada carro independente de fato se assemelham a uma reta sugerida pela Figura 3. Note também que as retas de cada carro são similares mas não são idênticas.
O coeficiente linear do carro 1 é $b_1 = 0,0463$ e do carro 2 é $b_2 = 0,0508$. Como os coeficiente linear deve ser tal que $b = \sin 2\theta/g$, se usamos $g = 9,81 m/s^2$, encontramos que a angulação da rampa para o carro 1 deve ser $\theta_1 = 13,51^o$, e para o carro 2 deve ser $\theta_1 = 14,95^o$. O valor real da angulação da rampa utilizada (medida com ajuda de uma régua) é de $\theta_{real} \approx 14,7^o$. Temos portanto um erro de aproximadamente 8% no carro 1, e de 2% no carro 2 na estimativa do ângulo de lançamento.
Já para o coeficiente independente, para o carro tem-se $c_1 = 0,0711$, e para o carro 2 $c_2 = 0,0448$. O coeficiente independente é tal que $c = L\tan \theta$. Usando-se os valores de ângulo estimados para cada carro, os valores estimados de $L$ são $L_1 = 1,11$ cm para o carro 1, e $L_2 = 1,36$ cm para o carro 2. O valor exato na pista é de $L = 5,5$ cm. Obtivemos portanto um erro grande da ordem de 75%.
Conclusões
Os dados do salto dos carrinhos estão de acordo com a física do lançamento oblíquo, pois o gráfico de $A$ vs $V_0^2$ representa uma linha reta, conforme previsto pela teoria do lançamento oblíquo. As medidas também apontam para um valor de ângulação da rampa muito próximo do valor do real (com erro máximo de 8%). Isto também indica que o salto do carrinho obedece à física do lançamento oblíquo que a aprendemos na escola.
Por outro lado, os valores estimados de $L$ apresentaram um erro muito grande comparado ao valor real da pista. Este erro pode ser melhorado se aumentarmos o número de lançamentos para cada carrinho, especialmente para baixas velocidades. A velocidade mais baixa medida para o carrinho 1 foi de 1,744 m/s (alcance de 21 cm), e de 1,388 m/s para o carrinho 2 (alcance de 14 cm). Seria necessário mais medidas com velocidade menores que estas para que a estimativa de $L$ fosse mais próxima do valor real da pista utilizada. Uma outra razão possível que a exigência $L<H$ para justificar a expansão de Taylor pode estar sendo violada, uma vez que a rampa utilizada tem uma angulação suave de apenas $14,7^o$. Neste caso, o termo independente $L/\tan \theta$ na fórmula do alcance precisa de correção.
De qualquer forma, estou satisfeito com os resultados obtidos e podemos concluir que o salto dos carrinhos Hotwheels obedecem sim às leis da física do lançamento oblíquo!
Assista aqui a demonstração em vídeo deste experimento: