August, 2021 - Fisicalidades

A física do loop

17/08/202117/08/2021 jeanlexdesousa 2 Comments

Looping é uma manobra bastante comum em esportes radicais e no entretenimento como no skate, em espetáculos de circo e até em videogames, como mostrado na Figura 1. Neste post, nós vamos discutir quais a condições necessárias para que o loop seja executado com segurança.

Figura 1: loop presente em manobras de skate, no globo da morte e no videogame.

A Física do loop

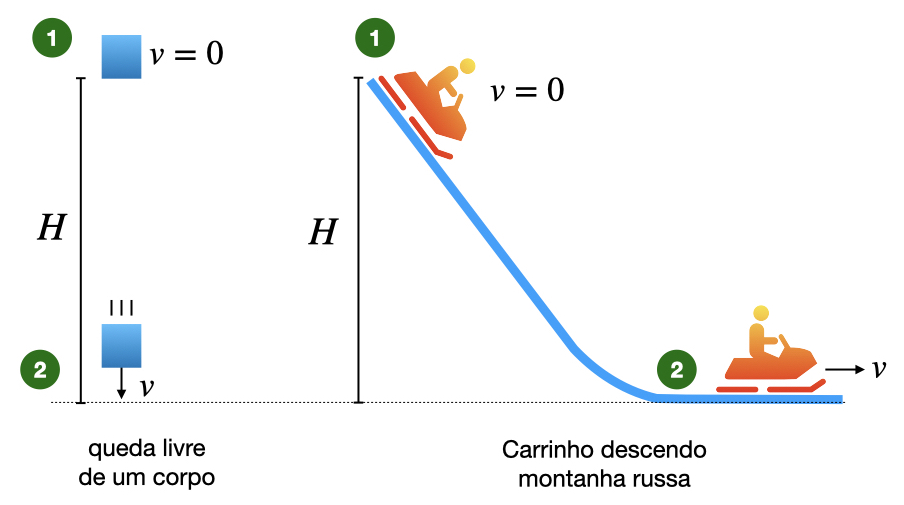
A Figura 2 mostra um sistema idealizado para estudarmos o looping. Para simplificar, assumimos que o loop é um círculo de raio $R$. Um corpo em repouso é liberado do ponto 1, localizado a uma altura H em relação ao solo, e desce até o nível do solo onde atinge uma velocidade $v_0$ momentos antes de entrar no loop. Nosso objetivo e determina a velocidade $v_0$ mínima para que possamos executar o looping sem cair.

No ponto mais alto do loop, o corpo tem uma velocidade $v_1$, e sai do loop com uma velocidade $v_2$. Assumimos também que o corpo não tem nenhum tipo de propulsão, e toda a velocidade de entrada no loop foi causada apenas pela elevação inicial do ponto 1.

Figura 2: sistema idealizado para estudar a Física do looping.

Vamos nos concentrar inicialmente entre os pontos 2 e 3. No ponto 2, o corpo possui apenas energia cinética, enquanto no ponto 3 possui energia cinética e energia potencial gravitacional. Assumindo que a energia mecânica total é conservada entre os pontos 2 e 3 ($E_{M,2}=E_{M,3}$), temos:

$$E_{M,2} = \frac{m v_0^2}{2}$$

$$E_{M,3} = \frac{m v_1^2}{2}+m g(2 R)$$

$$v_0^2 = v_1^2+ 4 R g.$$

Nas expressões acima, $m$ é a massa do corpo e $g$ é aceleração da gravidade. A última equação mostra que $v_0$ depende de $v_1$ e que, sozinha, esta equação não permite dizer nadinha sobre qual o valor de $v_0$ que permita executar o looping.

A condição necessária para que o o corpo execute o looping é NÃO PERDER CONTATO COM PISTA ! Enquanto houver contato, o corpo faz uma força sobre a pista que, pela 3a. lei de Newton, aplica uma força mesmo módulo mas na direção contrária no corpo. Esta forçado reação da pista sobre o corpo é a força normal $\vec{N}$. Desprezando-se qualquer tipo de atrito, a outra força atuando sobre o corpo é o seu peso $\vec{P}$. O diagrama de forças que atua no corpo no ponto mais alto do loop é mostrado na Figura 3.

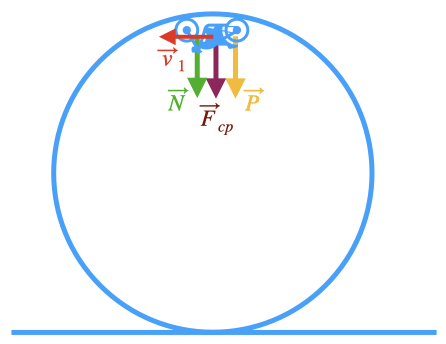
Figura 3: Diagrama de forças atuando no corpo no ponto mais alto do loop.

Devido ao movimento encurvado, o corpo está sujeito a uma força centrípeta resultante igual a soma vetorial de todas as forças atuando no corpo, ou seja, $\vec{F}_{cp}=\vec{N}+\vec{P}$. Como todos os vetores são colineares no ponto mais alto, tem-se portanto $F_{cp} = N+P$. A condição para que haja contato do corpo com a pista é que o módulo da força normal seja diferente de zero, ou seja, $N = F_{cp}-P>0$. Como $F_{cp} = m v_1^2/R$, a condição para que o corpo não perca contato com o loop é:

$$v_1^2 > R g.$$

Desta forma, a velocidade mínima de entrada para realizar o looping sem cair é:

$$v_0^2 > 5 R g.$$

Para concluir falta apenas determinar qual a altura mínima que devemos soltar o corpo na rampa para que ele complete loop. Para isso, assumimos mais uma vez que a energia mecânica total é conservada entre os pontos 1 e 2 $E_{M,1}=E_{M,2}$:

$$E_{M,1} = m g H$$

$$E_{M,2} = \frac{m v_0^2}{2}$$

$$v_0^2 = 2 g H.$$

Finalmente, a altura $H$ que o carro deve ser solto para completar o loop é:

$$H > 2,5 R.$$

E se houver atrito?

Na descrição acima, assumimos que a energia mecânica total se conserva em todo o trajeto do ponto 1 até o ponto 3. Contudo, vimos no post anterior que se houver qualquer tipo de atrito, um corpo solto de uma altura $H$ na rampa, ele vai chegar no ponto 2 com uma velocidade tal que $v_0^2 < 2 g H$. Portanto, para executar o loop basta soltar o corpo de uma altura um pouco maior para compensar a dissipação da energia mecânica pelo atrito.

Uma forma simples de quantificar este efeito é o seguinte. Imagine que a entre os pontos 1 e 2 hove uma perda e 5% de energia, e mais outros 5% entre os pontos 2 e 3. Portanto, temos que $E_{M,2} = 0,95 E_{M,1}$, e $E_{M,3} = 0,95 E_{M,2}$. Mesmo com atrito na pista, a condição para que o corpo não perca contato com a pista continua sendo $v_1^2 > R g$. Deixo como exercícios para os leitores, demonstrar que a nova altura para soltar o corpo e realizar o loop deve ser tal que $H > (2,5 R)/(0,95)^2$, ou mais precisamente $H > 2,77 R$. Ou seja, precisamos aumentar a altura em cerca de 10% para que o corpo consiga realizar o loop.

Finalmente o experimento

A Figura 4 mostra o experimento realizado para testar nossa teoria. O loop utilizado não é perfeitamente circular, e possui cerca de 24 cm de diâmetro. Portanto, a altura mínima para o carrinho conseguir fazer o looping sem cair é de aproximadamente 30 cm. Se assumirmos uma dissipação de energia mecânica de 5% entre os pontos 1 e 2, e outros 5% entre 2 e 3, a altura mínima será de 33 cm. Em termos de velocidade, a condição mínima para que os carrinhos realizassem o loop é que $v_0 > \sqrt{5 R g}$. Assumindo $g = 9,81~m/s^2$ e $R = 0,12~m$, a velocidade mínima para completar o loop é de aproximadamente $2,43~m/s$ ($8,7~km/h$).

Figura 4: Experimento para demonstrar a Física do looping utilizando uma pista Hotwheels. Testei 5 carrinhos. Os carrinhos 1, 2 3 têm os pneus bem balanceados. Oscarrinhos 4 e 5 estão desbalanceados e não conseguem andar em linha reta por muito tempo.

Neste experimento, utilizei 5 carrinhos Hotwheels diferentes, sendo que dois deles já estavam velhinhos e apresentavam desbalanceamento nos pneus e não conseguiam andar em linha reta muito tempo (carrinhos 4 e 5). Os carrinhos desbalanceados tendem a encostar nas bordas da pista, e atendem bem ao nosso intuito de testar o efeito do atrito.

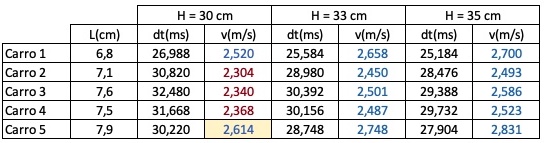
A tabela 1 mostra as velocidades medidas na entrada do loop para todos os carrinhos soltos em diferentes alturas: 30 cm (prevista pela teoria como a altura mínima necessária para o carrinho percorrer o loop sem cair), 33 cm e 35 cm (para testar a hipótese de dissipação de energia mecânica por atrito). As velocidades foram medidas utilizando o sensor de velocidade discutido no post Conservação da energia mecânica com Hotwheels e Arduino.

Quando soltos de uma altura ligeiramente acima de 30 cm, somente o carrinho 1 conseguiu completar o loop sem cair. A velocidade $v_0$ medida for de 2,52 m/s, um pouco acima do limiar teórico de 2,43 m/s. Nenhum dos outro carrinhos conseguiu percorrer o loop quando soltos de 30 cm. Neste grupo, os carrinhnos 2,3 e 4 apresentaram a velocidade de entrada no loop abaixo da velocidade limite e, portanto, não tinham energia suficiente para percorrer o loop sem cair. Contudo, o carrinho 5, apesar de ter caído, apresentou velocidade de entrada de 2,614 m/s, acima da velocidade mínima. É óbvio que este carrinho dissipa mais energia na subida do loop que os outros, pois ele é dos carrinhos que claramente apresentava um desbalançeamento das rodas.

Quando os carrinhos foram soltos de uma altura de 33 cm (10% acima da altura mínima prevista pela teoria), todos completaram o loop, sendo que alguns deles visivelmente completaram o loop com velocidade de entrada ligeiramente acima da velocidade limiar. Por exemplo, o carrinho 2 apresentou velocidade de entrada de 2,45 m/s, apenas 0,02 m/s acima da velocidade mínima. O mesmo foi observado nos carrinhos 3 e 4. Finalmente, quando soltos de uma altura de 35 cm, todos os carrinhos percorreram o loop confortavelmente sem cair, todos com velocidades de entrada acima da velocidade mínima.

Tabela 1: velocidades de entrada no loop dos carrinhos soltos a partir de alturas diferentes. As velocidade em azul (vermelho) estão acima (abaixo) da velocidade mínima teórica de 2,43 m/s necessária para percorrer o loop sem cair. Obs: Para o lançamento de 30 cm, o carrinho 5 apresentou velocidade de entrada acima de 2,43 m/s, mas caiu do loop. O carrinho 5 parece dissipar mais energia mecânica que os outros carrinhos na subida do loop.

Em conclusão, nosso experimento demonstrou que as condições necessárias para percorrer o loop sem cair, ou seja, uma velocidade de entrada $v_0>\sqrt{5 R g}$ garante que o carrinho passe pelo ponto mais alto do loop sem perder contato com a pista. foram comprovadas experimentalmente, apesar da pequena dissipação de energia mecânica por atrito. Para garantir esta velocidade de entrada, basta soltar o carrinho de uma altura $H> 2,5 R$. O nosso melhor carrinho (o carrinho 1) satisfez perfeitamente as previsões teóricas, enquanto os ouros carrinhos precisaram de uma elevação inicial até 10% maior para ganhar velocidade suficiente para percorrer o loop sem cair.

Preciso fazer três observações importantes: (i) o loop é flexível e pode balançar durante a passagem, e fazer com que o carrinho caia da pista. O ideal é colocar um suporte para minimizar o balanço da pista e usar fita adesiva para fixar o loop na mesa. Mesmo assim ele vai balançar. (ii) O sensor de velocidade precisa ser fixado na pista sem balançar. O movimento do sensor durante a passagem do carrinho pode afetar as medidas de velocidade. (iii) As medidas da altura foram feitas com fita métrica simples, e portanto sujeitas a pequenas variações tanto na medida da altura quanto no ponto em que o carrinho foi solto. Estas duas fontes de imprecisão fazem com que haja pequenas variações de velocidade em cada lançamento até mesmo quando usamos o mesmo carrinho. O ideal é fazer uma média de 3 ou 4 lançamentos para cada carrinho e fazer uma média aritmética simples. Mas não se preocupem, flutuações existem até mesmo em laboratórios de alta tecnologia, mas o importante é que elas não sejam grandes o suficiente para apontar um resultado que seja incompatível com o modelo utilizado para explicar o experimento.

Assista aqui a demonstração em vídeo deste experimento:

Conservação da energia mecânica com Hotwheels e Arduino

06/08/202109/08/2021 jeanlexdesousa 1 Comment

O nosso sensor de passagem para medir velocidade continua rendendo várias experiências interessantes e divertidas. No posto de hoje vamos falar sobre conservação de energia mecânica utilizando novamente uma pista de carrinhos Hotwheels e um sensor de velocidade.

Tipos de energia mecânica

Energia mecânica é todo tipo de energia associada ao movimento e/ou posição dos corpos. Na escola a gente aprende que há dois tipos de energia mecânica:

Energia cinética: um tipo de energia que está associada ao movimento dos corpos. Se um corpo de massa $m$ se move com velocidade $v$, este corpor possui uma energia cinética $E_C$ dada por:

$$E_C = \frac{m v^2}{2}$$

Energia potencial: um tipo de energia que está associado a posição de um objeto em relação a algum tipo de campo de força que interaja com o objeto. Na escola, a gente aprende que há 3 tipos de energia potencial: energia potencial gravitacional, energia potencial elástica, e energia potencial elétrica. Em outras oportunidades iremos discutir mais especificamente as diferentes formas de energia potencial, mas neste post iremos focar apenas na energia potencial gravitacional. Sabemos que qualquer objeto ou ser vivo em nosso planeta está sujeito ao campo gravitacional da Terra. Se elevarmos e soltarmos um objeto de massa $m$ a uma altura $H$ do solo, sabe-se que este objeto vai cair. E quanto mais alta for a altura $H$, maior vai ser a velocidade com que o objeto atinge o solo. Antes de o objeto adquirir energia cinética devido ao movimento de queda, o objeto ganhou energia potencial gravitacional dada por:

$$U_g = m g H$$

Conservação da energia mecânica

Um princípios mais importantes que regem tudo o que existe no universo é o da conservação da energia, seja ela mecânica ou não-mecânica. Quando não há forças que dissipem energia, toda a energia mecânica é conservada. Vejamos os exemplos dados na Figura 1.

Figura 1: (esq.) Corpo em queda livre. (dir.) Carrinho descendo uma montanha russa.

A Figura 1 mostra dois casos: a queda livre a esquerda, e de um carrinho descendo uma montanha russa. Nos dois casos, o corpo está parado e a uma altura $H$ em relação ao solo. A energia mecânica total do corpo no ponto 1 é:

$$E_{M,1} = E_{C,1} + U_{g,1} = 0 + m g H = m g H.$$

Como o corpo está parado no ponto 1, sua velocidade é nula ($v_1 = 0$), portanto, sua energia cinética também é zero ($E_{C,1}=0$). No ponto 2, o objeto está a uma altura zero em relação ao solo, e se movendo com uma velocidade $v_2$ que desconhecemos. Portanto, sua energia mecânica total é dada por:

$$E_{M,2} = E_{C,2} + U_{g,2} = \frac{m v_2^2}{2} + 0 = \frac{m v_2^2}{2}.$$

Se não houver nenhum tipo de força que dissipe energia mecânica (força de atrito com o ar e/ou com o trilho, por exemplo), a energia mecânica total do sistema será conservada, ou seja, será a mesma para os pontos 1 e 2 ($E_{M,1}=E_{M,2}$). Se soubermos a altura $H$ inicial, podemos tirar proveito da conservação da energia mecânica e determinar a velocidade no ponto 2:

$$m g H = \frac{m v_2^2}{2} ~~ \rightarrow ~~ v_2^2 = 2 g H$$

O mais surpreendente desse resultado é que ele independe da massa $m$ do objeto, e também do caminho total percorrido pelo objeto. Note que na queda livre, o corpo percorre apenas uma distância $H$, que é altura de onde o corpo cai. No caso da montanha russa, o carrinho percorre o comprimento $L$ entre os pontos 1 e 2 da pista, que é maior que a altura inicial $H$. Isto só acontece porque o campo gravitacional é dito conservativo (ou seja, conserva energia mecânica), e o que interessa de fato são apenas as posições inicial e final do objeto em relação a superfície da Terra, e não o caminho percorrido.

E se houver forças dissipativas?

Se, em qualquer uma das situações mostradas na Figura 1, houver forças que dissipem a energia mecânica do sistema como a força de resistência do ar e/ou força de atrito com o trilho da montanha russa, a energia mecânica total não será conservada. Neste caso, teremos $E_{M,1} \neq E_{M,2}$. Mas é interessante saber o que ocorre com a diferença de energia mecânica entre os pontos 1 e 2:

$$ \Delta E_M = (E_{C,2}+U_{g,2})- (E_{C,1}+U_{g,1}) = \Delta E_C + \Delta U_g $$

A equação acima mostra que a variação de energia mecânica é simplesmente a soma das variações de todos os tipos de energia mecânica. No nosso caso específico da Figura 1, temos que

$$ \Delta E_M = \frac{m v_2^2}{2}~-~m g H.$$

Agora pensemos o seguinte, se houver qualquer tipo de atrito (com o ar e/ou trilho), a velocidade no ponto 2 será menor que na situação em que não há atrito. Portanto, obteremos $\Delta E_M < 0$ sempre !!!! Por outro lado, se $\Delta E_M >0$, é porque a velocidade do corpo no ponto 2 é maior do que quer deveria ser na situação em que não há atrito. E isso só pode ocorrer com uma única condição, houve alguma forma de energia dada ao corpo que serviu de propulsão para ganho de velocidade !!!

O experimento

Para estudar a conservação da energia mecânica, vamos utilizar o experimento mostrado na Figura 2, onde simulamos um trecho de queda de uma montanha russa. Vamos soltar dois carrinhos (de massas diferentes) de várias alturas diferentes, e medir sua velocidade na parte horizontal da pista.

Se houver conservação de energia mecânica no nosso experimento, sabe-se que $v_1^2 = 2 g H$, então o gráfico $v_1^2$ vs $H$ construído com os dados de cada lançamento deve ser uma linha reta cujo coeficiente linear é igual a $2 g$, independente portanto da massa do carrinho. Se os dados experimentais ficarem abaixo desse gráfico, é porque há algum tipo de atrito no nosso experimento. Se ficarem acima, é porque há algum tipo de propulsão sendo dada aos carrinho, conforme mostrado na Figura 3.

Figura 3: Diagrama de $V^2$ vs $H$ mostrando as regiões de ganho, conservação e dissipação de energia.

Medidas

A Figura 4 mostra a tabela dos dados medidos para dois carrinhos diferentes (os mesmos do post anterior sobre a física do lançamento oblíquo). Ao todo foram realizados 10 lançamentos variando entre uma altura mínima de 25,5 cm e uma altura máxima de 57,5 cm.

É interessante notar que os dados dos dois carrinhos são idênticos, apesar das massas e tamanhos diferentes, e apresentando os valores de $v^2$ ligeiramente abaixo da linha teórica de conservação de energia. Para o lançamento de $H$ = 57,5 cm, a perda de energia é de menos de 1%, já para $H$ = 25,5 cm, a perda de energia é de cerca de 13%. No nosso sistema há três mecanismos principais de dissipação de energia: atrito nos pneus dos carrinhos, atrito com a pista, e a resistência do ar. Em princípio, é basta difícil separar a contribuição de cada um destes efeitos sem a montagem de experimentos mais sofisticados.

É importante também mencionar que há outra contribuição de energia mecânica que não foi considerada no problema: a energia cinética associada a rotação dos pneus. Embora este efeito seja bem complicado de explicar sem um experimento mais detalhado, acredito que esta contribuição é muito pequena devido ao pequeno diâmetro dos pneus, e tem pouco impacto nos resultados.

Apesar do pequeno efeito de dissipação de energia mecânica, concluo que, em uma primeira aproximação, podemos considerar que a energia mecânica foi conservada neste experimento.

Assista aqui demonstração deste experimento em vídeo:

Observação sobre a medida da velocidade

Neste experimento, a velocidade foi medida usando o sensor de passagem descrito aqui, mas com uma pequena modificação. Como foram feitas muitas medidas em alturas muito próximas umas das outras, foi necessário mudar o código do Arduino para que ele medisse os tempos de passagem com precisão de microssegundos. Utilizamos o mesmo código descrito aqui, mas trocando a chamada da função millis() pela função micros(). Segue abaixo o código utilizado para medir tempos de passagem com precisão de microssegundos.

// Definição das entradas

// define o pino digital 3 como entrada do fototransistor
const int FOTOpin = 3; 
bool ligado = false;
long dt;

void setup() {
 // coloque aqui o código de inicialização que será executada apenas uma vez.
  
  // configuração do pino 3 como entrada
  pinMode(FOTOpin, INPUT); 

  // inicializa a saída serial do Arduino
  Serial.begin(9600); 
 
}

void loop() {
  // put your main code here, to run repeatedly:

  // leitura do fotodiodo
  int v1 = digitalRead(FOTOpin); 

  // detecta se um objeto chegou no sensor
  if ((v1 == HIGH) & (ligado == false)){
    ligado = true;
    dt = micros();
  }  

  // detecta se um objeto saiu do sensor
  if ((v1 == LOW) & (ligado == true)){
    ligado = false;
    dt = micros() - dt;
    Serial.print("Tempo de passagem (micro seg.) = ");
    Serial.println(dt);
  }  

}