Depois de várias semanas sem conseguir publicar nada, vamos voltar em grande estilo. No post de hoje vamos demonstrar como provar a 2a. lei de Newton utilizando apenas um sensor de velocidade, moedas, carrinhos a acessórios Hotwheels. Mas antes, vamos rever rapidamente a teoria.
O básico da 2a. lei de Newton
A segunda lei de Newton diz que um corpo de massa $m$ sujeito a uma força resultante $\vec{F}_R$ se move com aceleração $\vec{a}$ definida por:
$$\vec{F}_R = m \vec{a}.$$
A força $\vec{F}_R$ e a aceleração $\vec{a}$ são grandezas vetoriais e apontam sempre na mesma direção. A expressão acima é bem geral e vale tanto para movimento em linha reta ou curvilíneo. Um detalhe importante é que $\vec{F}_R$ é a força resultante, ou seja, é a combinação (soma vetorial) de todas as forças atuando no corpo de massa $m$ que produz a aceleração $\vec{a}$. Além disso, a expressãoo acima permanece válida mesmo que a força e a aceleração variem no tempo, mas a massa deve ser uma constante. Para os casos em que a massa é variável (ex.: lançamento de um foguete), a 2a. lei de Newton é escrita da seguinte forma:
$$\vec{F}_R = m \frac{d \vec{p}}{d t} = m \vec{a} + \frac{d m}{ dt} \vec{v},$$
onde $\vec{p}= m \vec{v}$ é o momento linear do corpo, e $d m/d t$ é taxa de variação da massa do corpo. Mas neste post, nós vamos nos estudar apenas o caso em que a massa permanece constante.
A aceleração é a quantidade física que descreve quão rápido a velocidade de um corpo muda, e é definida como:
$$\vec{a} = \frac{\Delta \vec{v}}{\Delta t} = \frac{\vec{v}_f-\vec{v}_i}{\Delta t}.$$
onde $\vec{v}_i$ e $\vec{v}_f$ representam as velocidades inicial e final, respectivamente, e $\Delta t$ é um intervalo de tempo.
Olhando para as equações acima, precisamos ser capazes de medir aceleração, força, e massa para demonstrar a 2a. lei de Newton. Medir massa é simples, podemos utilizar uma balança de cozinha dessas bem baratinhas. Porém, medir forças é mais complicado pois precisamos de sensores específicos que não disponho no momento. Já a aceleração pode ser medida com acelerômetros (também mais complicados e que merecerem um post só para falar deles), ou com sensores de velocidade destes que uso aqui no blog.
No caso mais geral, precisamos de dois sensores para medir as velocidades $\vec{v}_i$ e $\vec{v}_f$, e também medir o tempo $\Delta t$ que o objeto leva para ir de um sensor ao outro. Embora não seja nada exorbitante complicado usar dois sensores com Arduino, a ideia deste post é bolar um experimento para provar a 2a. lei de Newton com um único sensor de velocidade e sem nenhum sensor de força.
Desenhando o experimento
Imagine a situação mostrada na Figura 1. Você coloca um corpo de massa $m$ e comprimento $L$ parado imediatamente atrás da linha de ação do sensor de velocidade. No instante $t=0$ um dispositivo qualquer aplica subitamente uma força desconhecida $F$ sobre o corpo, e ele começa a se mover ativando o sensor de velocidade. Em um instante posterior $t = \Delta t$ o corpo cruza inteiro a linha de detecção do sensor. Neste instante o corpo está com uma velocidade $v$. Desta forma sabemos as velocidades do corpo exatamente antes ($v_i=0$), e exatamente depois do corpo cruzar o sensor de velocidade $v_f=v$, e o tempo $\Delta t$ em que houve variação de velocidade.
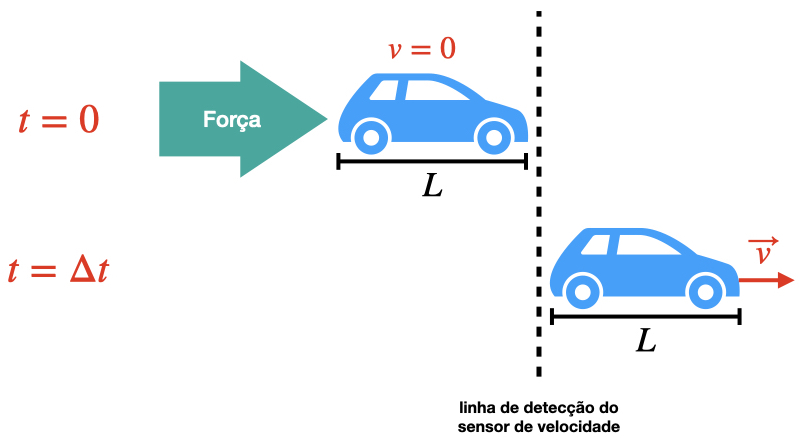
Assumindo que somente a força $F$ atuou sobre o corpo, podemos então aplicar a 2a. lei de Newton (em uma dimensão) e determinar o valor de $F$:
$$F = m a = m \frac{\Delta v}{\Delta t} = m \frac{v-0}{\Delta t}=\frac{m v}{\Delta t}.$$
Ora, mas $v$ é a velocidade instantânea do carro ao passar pelo sensor e pode ser determinada como:
$$v=\frac{L}{\Delta t}.$$
Daí, o valor desconhecimento de $F$ pode ser determinado como:
$$F = \frac{m L}{\Delta t^2}.$$
Os parâmetros $m$, $L$ e $\Delta t$ são facilmente determinados com uma balança de cozinha, uma fita métrica e com o nosso sensor de velocidade feito com Arduino.
O experimento
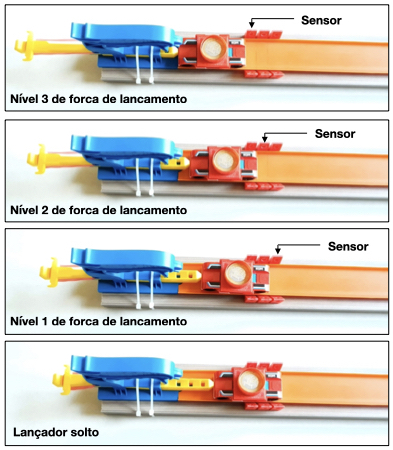
Mais uma vez vamos utilizar carrinhos e acessórios Hotwheels para construir nosso experimento, e provar a 2a. lei de Newton. A Figura 2 mostra o arranjo experimental com 2 segmentos de pista, um lançador de carrinhos de elástico com 3 níveis de força, um suporte para o sensor e o sensor de velocidade. Nos meus testes, percebi que o lançador e a pista precisam ficar bem fixos e se mexer o mínimo possível em cada lançamento. Por isso prendi tudo com braçadeiras plásticas.

Percebi também alguns problemas com este arranjo experimental:
PROBLEMA 1: Pelo tipo de lançador baseado em elásticos, a cada nível de força o elástico estica mais, e o carrinho é lançado de um ponto mais atrás, conforme mostra a Figura 3. O ideal é que o carrinho comece o movimento a uma distância fixa do sensor, independente do nível de força do lançamento.
PROBLEMA 2: Ajusta o sensor, medir o tamanho do carro, a massa dele, o tempo $\Delta t$ de cada lançamento, e substituir na fórmula vai sim fornece um número com unidades de força, mas não é uma prova da lei de Newton. Para provar que $F=m a$ é válida, seria necessário confirmar que a força $F$ exercida pelo lançador sobre o carrinho é numericamente igual a $m L/\Delta t^2$. Mas não temos um sensor de força ainda!
Somos pessoas criativas e podemos driblar o a falta de um sensor de força com conhecimento. A 2a. lei diz que $F_R = m a$, mas só temos os meios de medir $m$, $L$ e $\Delta t$, e uma lançador com 3 níveis de força desconhecidos. Mas se a 2a. lei estiver correta, podemos realizar vários lançamentos mantendo fixo o nível de força em carrinhos com diferentes massas $m$, e medir a respectiva aceleração de cada carrinho. Como $a = F_R/m$, se plotarmos $a~versus~m^{-1}$, o gráfico dever ser uma reta cujo coeficiente linear é o valor da força. Como os níveis de força do lançador são tais que $F_{R,3}>F_{R,2}>F_{R,1}$, o gráfico dos lançamentos com carrinhos de diferentes massas deve se parecer com a Figura 4.
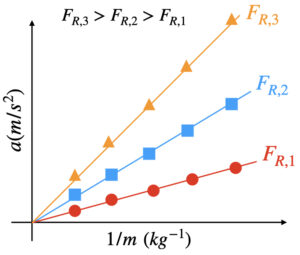
Se o gráfico medido for uma reta, então a 2a. lei está provada. E de quebra podemos ainda conhecer a intensidade de cada nível de força do lançador.
PROBLEMA 3: Nosso experimento vai determinar a força resultante, ou seja, a combinação de todas as forças atuando sobre o carrinho, incluindo o atrito. Já sabemos que nenhum carrinho é igual ao outro e possuem níveis de atrito diferentes. Para manter sobre controle o atrito, vamos utilizar um carrinho especial modificado, mostrado na Figura 5. Este carrinho foi fabricado para levar a câmera Gopro Sessions (já descontinuada) e fazer vídeos radicais. Para ver este carrinho em ação clique aqui.
Achei esse carrinho numa loja de brinquedo por menos de R$ 10,00. Mas em vez da câmera, adaptei um suporte para moedas de 1 Real, e fiz a massa variar aumentando o número de moedas. Cada moeda possui 7g de massa, e para cada curva fiz 8 medidas, variando o peso do carrinho de 0 até 7 moedas. Especificamente, a massa varia de 45 g até 94 g em passos de 7g. Uma curva com 8 pontos é suficiente para mostrar uma bela linha reta se ela existir.

As medidas
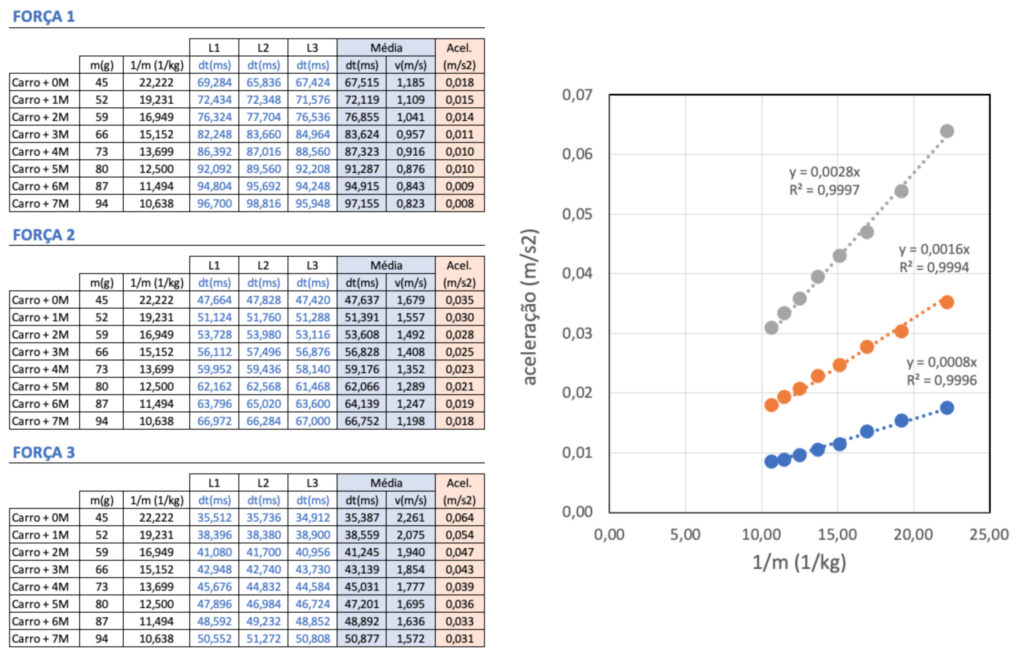
Para melhorar ainda mais a precisão, decidi fazer 3 lançamentos para cada massa e nível força, tirar a média aritmética dos tempos de passagem $\Delta t$, e com ele calcular a velocidade e aceleração. Todos os dados medidos estão na Figura 6. É fácil perceber que as os dados medidos formam linhas retas quase perfeitas. Os dados em azul representam os lançamentos com nível de força 1, os dados laranja representam os lançamento com nível de força 2, e os dados cinza representam os lançamentos com o nível de força 3.
De acordo com a nossa teoria, o coeficiente linear das curvas representa a força resultante de cada nível de força. Em particular, obtive $F_{R,1} = 0,0008~N$, $F_{R,2} = 0,0016~N$, e $F_{R,1} = 0,0028~N$. Conforme esperado, estes valorem obedecem $F_{R,3} > F_{R,2} > F_{R,1}$.
Finalmente, podemos concluir que este experimento muito simples que utiliza somente um sensor de velocidade reproduziu muito bem o comportamento previsto pela 2a. lei de Newton. Confesso que fiquei surpreso com a qualidade dos resultados, mesmo com a limitação auto-imposta de usar apenas um sensor.
Medidas mais precisas da aceleração podem ser obtidas combinando-se 2 sensores de velocidade. Mas isto é assunto para posts futuros.
Veja a demonstração em vídeo aqui (modificado em 08/11/2021):