A força de atrito é tratada superficialmente nos livros e problemas de Física, e é praticamente inexistente nas aulas de laboratório. Mas, a menos que você esteja para vácuo do espaço, é praticamente impossível se livrar das forças de atrito.
Na minha época de estudante, a força de atrito me intrigava por uma simples razão. Por que a força de atrito é matematicamente definida como $F_{at} = \mu N$ ($\mu$ é o coeficiente de atrito, e $N$ é a força normal), se ela aponta na direção oposta ao movimento, mas a força $N$ é perpendicular ao movimento? Esta é a pergunta que motivou este post.
O objetivo deste post objetivo é desenvolver um experimento muito simples para estudar a força de atrito e distância de frenagem com Hotwheels, e provar que $F_{at} = \mu N$. Vamos também aprender a determinar o coeficiente de atrito dos carrinhos.
Um pouco de teoria
Imagine um veículo se movendo em uma estrada horizontal com velocidade $v$, e que aciona o freio bruscamente ao ver um obstáculo a uma certa distância a frente na estrada. Qual distância o carro vai percorrer até parar?
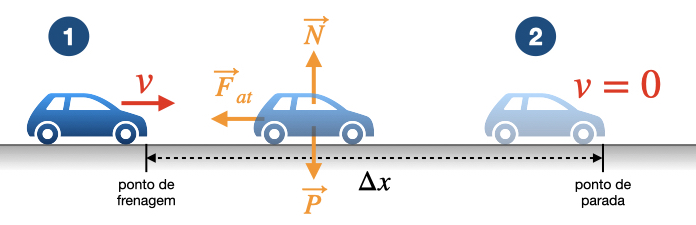
A Figura 1 mostra o diagrama deste problema. No ponto 1, o veículo está com velocidade $v$ e aciona o freio. Sem entrar nos detalhes mais complexos dos mecanismos de freio, durante o período de frenagem o carro está sujeito apenas às forças peso $\vec{P}$, a força normal $\vec{N}$ e a força de atrito $\vec{F}_{at}$.
As forças $\vec{P}$ e $\vec{N}$ atuam na direção vertical e se anulam pois, além de apontarem em direções opostas, não há nenhum movimento nesta direção. Portanto, a força resultante que atua no carro é apenas a força de atrito $\vec{F}_R = \vec{P} + \vec{N} + \vec{F}_{at} = \vec{F}_{at}$.
O teorema trabalho e energia cinética noz diz que o trabalho da força resultante $W_R$ entre os pontos 1 e 2 é igual à variação da energia cinética entre estes pontos:
$$W_R = E_{C,2} – E_{C,1}.$$
Para simplificar a matemática, assumimos que a força de atrito é constante durante toda a distância de frenagem. Desta forma, o trabalho da força resultante $\vec{F}_R$ é calculado como
$$ W_R = \vec{F}_R \cdot \Delta \vec{x} = \vec{F}_{at} \cdot \Delta \vec{x} $$
onde $\Delta \vec{x}$ é o vetor deslocamento (e que aponta na direção do movimento). Esta equação possui uma operação vetorial chamada de produto escalar, mas não se assustem. O significado é mais simples do que parece.
O produto escalar entre dois vetores $\vec{A}$ e $\vec{B}$ é dado por $\vec{A}\cdot\vec{B} = |\vec{A}||\vec{B}|\cos \theta$, onde $|\vec{A}|$ é o módulo do vetor $\vec{A}$, e $\theta$ \e o ângulo entre $\vec{A}$ e $\vec{B}$. Como $\Delta \vec{x}$ e $\vec{F}_{at}$ apontam em direções opostas, o ângulo entre estes vetores é de $180^o$, cujo cosseno é igual a $-1$. Desta forma, o trabalho da força de atrito é negativo:
$$W_{at} = – F_{at} \Delta x$$
O sinal negativo significa que o a força de atrito atua na direção contrária ao movimento. Se esta força atuasse na mesma direção do movimento, o trabalho teria sinal positivo.
Mas no nosso problema específico, a variação de energia cinética também é negativa $E_{C,2}-E_{C,1} = 0 – m v^2/2$. Combinando-se estes dois resultados, encontramos que o módulo da força de atrito durante a frenagem é dado por:
$$F_{at} = \frac{m v^2}{2 \Delta x}.$$
Nós aprendemos na escola que $F_{at} = \mu N$, onde $\mu$ é o coeficiente de atrito. Como nosso problema ocorre inteiramente na horizontal, temos que $N=P = m g$ ($g$ é a aceleração da gravidade). Daí, temos que:
$$F_{at} = \mu m g$$.
Observando cuidadosamente as duas equações acima, é possível propor uma forma simples de provar que a força de atrito é, de fato, proporcional à força normal (ao menos no problema do movimento completamente horizontal !).
Se usarmos um carrinho que pode carregar pequenos pesos (usei o mesmo do post sobre a 2a. lei de Newton), e assim variar sua massa, podemos realizar o experimento de distância de parada para massas diferentes e plotar o gráfico $F_{at} \times m$. Devemos então obter os resultados experimentais recaindo sobre uma linha reta como mostrado na Figura 2.
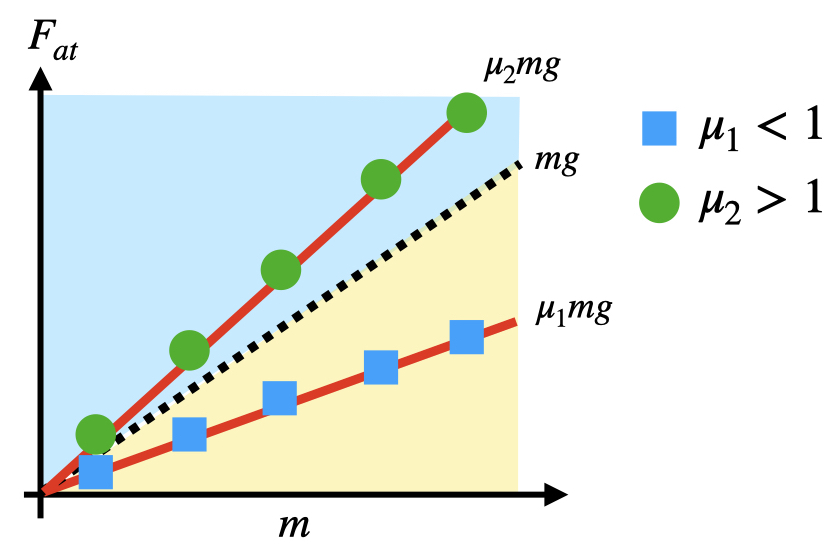
Na Figura 2, a linha tracejada representa a força peso $P$. Se os dados de de $F_{at} \times m$ recaírem sobre uma linha reta, temos que $F_{at} \propto N$ pois $P = N$ no movimento horizontal. Neste caso, o coeficiente da reta dever ser $\mu g$ pois $F_{at} = \mu m g$. Além disso, se os dados experimentais recaírem abaixo da linha da força $P$, o coeficiente de atrito do carrinho é menor que 1. Se os dados recaírem sobre uma linha acima da linha de $P$, é porque o coeficiente de atrito do carrinho é maior que 1. Chamo aqui a atenção para um fato muito importante: o coeficiente de atrito é uma grandeza adimensional !!!
O Experimento
De acordo com nosso modelo teórico descrito, precisamos lançar o carrinho com uma velocidade $v$, e medir a distância $\Delta x$ entre o ponto que a velocidade foi medida, e o ponto em que o carrinho parou. Estes dois valores são então substituídos nas equações acima para determinar a força de atrito. O setup experimental usado é mostrado na Figura 3.

Utilizei um único sensor de velocidade posicionado a uma pequena distância do ponto de lançamento do carrinho. Após o lançamento, a velocidade do carrinho é medida pelo sensor, e ele então percorre uma distância $\Delta x$ até parar. Utilizei o lançador e carrinho que pode levar várias moedas de 1 R$ do post anterior como forma de ter controle sobre a massa de um único carrinho, afim de evitar variações de coeficientes de atrito entre carrinhos diferentes. Este lançador possui 3 níveis de força e é capaz de aplicar forças resultantes da ordem de 0,8 mN, 1,6 mN e 2,8 mN, respectivamente. É importante lembrar que $\Delta x$ precisa ser medido entre o sensor e a traseira do carrinho.
Para minha surpresa, o carrinho com 7 moedas (cerca de 95 gramas) lançado no nível 2 de força percorre cerca 3,7 m antes parar. Isso mostra como o coeficiente de atrito dos carrinhos Hotwheels é baixo! Para o carrinho mais leve (cerca de 45 g), precisei de 11m de pista. Impressionante !!! Veja abaixo um exemplo de lançamento.
Para termos ideia do coeficiente de atrito, podemos usar como exemplo os dados de lançamento do vídeo acima. O carrinho com 94g passou pelo sensor com 1,19 m/s, e percorreu 3,7 m antes de parar. Se o modelo teórico estiver correto, o coeficiente de atrito é dado por $\mu = v^2/(2 g \Delta x) \approx 0,019$. De fato, é um valor muito pequeno. Mas lembre-se que a estimativa acima ainda não prova que $F_{at} \propto N$!
Dados experimentais
A Figura 4 mostra os dados medidos de força de atrito em função da massa do carrinho medida individualmente para cada nível de força do lançador. A massa do carrinho varia entre 45 g (sem nenhuma moeda) e 94 g (levando 7 moedas), em incrementos de 7 g (equivalente ao peso de uma moeda de 1 R$). As forças de atrito variaram entre 9 mN e 20 mN, confirmando que o atrito sobre os carrinhos é muito pequeno. Um detalhe importante, dada a grande quantidade de dados, é que fiz apenas um lançamento para cada combinação de massa e nível de força para simplificar a análise.
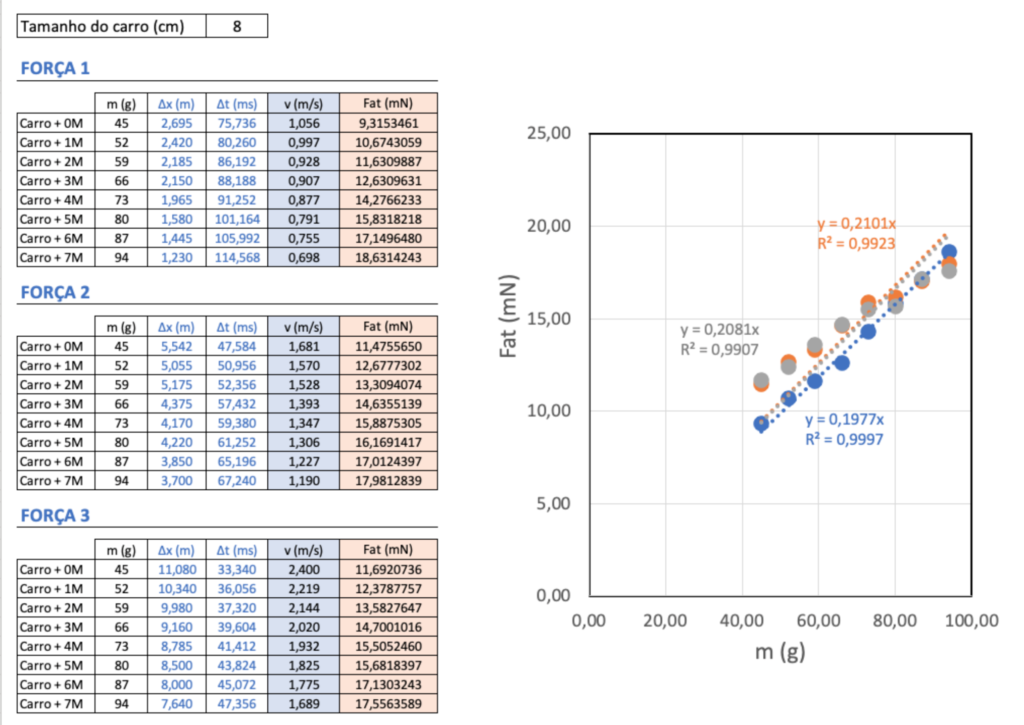
As medidas mostram que $F_{at}$ cresce linearmente em relação a massa, confirmando que $F_{at} \propto N$ no movimento horizontal. Além disso, os coeficientes lineares obtidos para cada nível de força do lançador são bastante parecidos: 0.1977 (nível 1), 0,2101 (nível 2) e 0,2081 (nível 3). Lembrando-se que, de acordo com a teoria $F_{at} = \mu m g$, o coeficiente linear da reta que descreve $F_{at} \times m$ é dados por $\mu g$. Precisamos ainda dividir os coeficientes das retas por $g = 9,81 m/s^2$ para obter os valores de $mu$.
Os valores obtidos de $\mu$ são: 0,020 (nível 1), 0,021 (nivel 2) e 0,021 (nível 3). Ou seja, os coeficientes de atrito obtidos para cada nível de força são idênticos. Mas isso é natural, já que usamos o mesmo carrinho, e o atrito deve ser o mesmo, independente do nível de força do lançamento.
Há uma pequena discrepância entre os dados do lançamento do nível 1, em relação aos níveis 2 e 3, quando o carrinho está mais leve, mas esta diferença é muito pequena. Uma razão possível para esta discrepância é que o carrinho mais leve lançado nos níveis de força 2 e 3 percorre muitos metros a mais pista comparado com o carrinho mais pesado e/ou lançado no nível 1. Quanto maior a força do lançamento, maior a distância percorrida pelo carrinho, e maiores são as chances do carrinho tocar nas laterais da pista, aumentando assim o coeficiente de atrito efetivo. Um outro detalhe que certamente faz diferença é que quanto maior o $\Delta x$, maior é o número de junções de pista que o carrinho vai atravessar. E estas junções não são perfeitamente alinhadas. Isto também ajuda a desacelerar o carrinho um pouco mais rápido. Veja no vídeo 2 o carrinho sofrendo pequenas variações de trajetória ao passar pelas junções e ao bater nas laterais da pista.
Nos meus testes, percebi variações de até 50 cm na distância de frenagem para lançamentos realizados com a mesma massa no nível 3 de força. Fazer a média de vários lançamentos para cada combinação de força de lançamento e massa, deve eliminar estas discrepâncias. Fixar a pista no chão com fita adesiva também ajuda a prevenir vibrações que podem aumentar a chance contato do carro com as bordas da pista.
Conclusões
O experimento descrito neste post nos permitiu demonstrar que $F_{at} = \mu N$ no movimento horizontal. Para isso, partimos apenas de um único principio fundamental: o teorema trabalho – energia cinética. Além disso, assumimos que a força de atrito era constante durante toda a distância de frenagem, e não levamos em conta o movimento de rotação dos pneus dos carrinhos, mas nada disso invalida qualitativa e quantitativamente os resultados obtidos aqui.
Para melhorar a precisão dos experimentos, convido os leitores a reproduzir o experimento realizando vários lançamentos para cada massa e nível de força, e construir os gráficos com os valores médios.
Um outro detalhe importante: para facilitar a coleta dos dados, usei um pequena tela OLED para projetar os valores dos tempos de passagem sem precisar monitorar as medidas pelo computador. Desta forma, o sensor de velocidade torna-se completamente independente do computador, e funciona como uma unidade portátil de realização de experimentos. Decidi não mostrar como se faz isto neste post, pois ele já está longo demais, mas prometo escrever um post sobre como fazer isso.
Finalmente, e não menos importante, o nosso experimento apenas prova que $F_{at} = \mu N$ é valida no movimento horizontal. A prova desta equação para movimento em pistas inclinadas, e portanto, em qualquer situação será assunto para o próximo experimento.