Motivado pelo post da Física do loop, no qual alguns dos carrinhos não foram capazes de completar o loop quando soltos da altura mínima, resolvi comparar o coeficiente de atrito de vários carrinhos Hotwheels repetindo o experimento do post anterior sobre a distância de frenagem.
De forma muito muito resumida, considere um veículo se movendo em uma estrada horizontal com velocidade $v$, e que aciona o freio bruscamente. Este carro irá percorrer uma distância $\Delta x$ antes de parar. Como já sabemos, $F_{at} = \mu N$ é valido para o movimento horizontal, e com a ajuda do teorema do trabalho e energia cinética, é possível determinar coeficiente de atrito. As fórmulas usadas estão mais a frente neste post.
O experimento é muito simples, e pode ser visto no vídeo abaixo. O carrinho é lançado por um lançador de elástico com três níveis de força. Os parâmetros medidos no experimento são apenas dois: (i) a velocidade $v$ do carro é medida pelo sensor de velocidade, e a a distância de parada $\Delta x$ medida em relação à posição do sensor de velocidade.
Nós vamos medir o coeficiente de atrito de 10 carrinhos diferentes, mostrados na figura abaixo. Apenas um lançamento foi realizado para cada nível de força do lançador. Para melhorar a precisão dos resultados, seria necessário realizar a média de vários lançamentos (3 a 5 para cada nível de força já seria o suficiente).

Os dados medidos estão nas tabelas abaixo agrupados por nível de força. As duas primeiras colunas são a massa e o tamanho do carrinho. Em seguida, a distância $\Delta x$ percorrida em cada lançamento, o tempo $\Delta t$ e a velocidade $v$ de passagem pelo sensor, a força de atrito e o coeficiente de atrito com as expressões abaixo:
$$F_{at} = \frac{m v^2}{2 \Delta x},$$
$$\mu = \frac{v^2}{2 g \Delta x}$$,
onde assumimos $g = 9,81~m/s^2$.
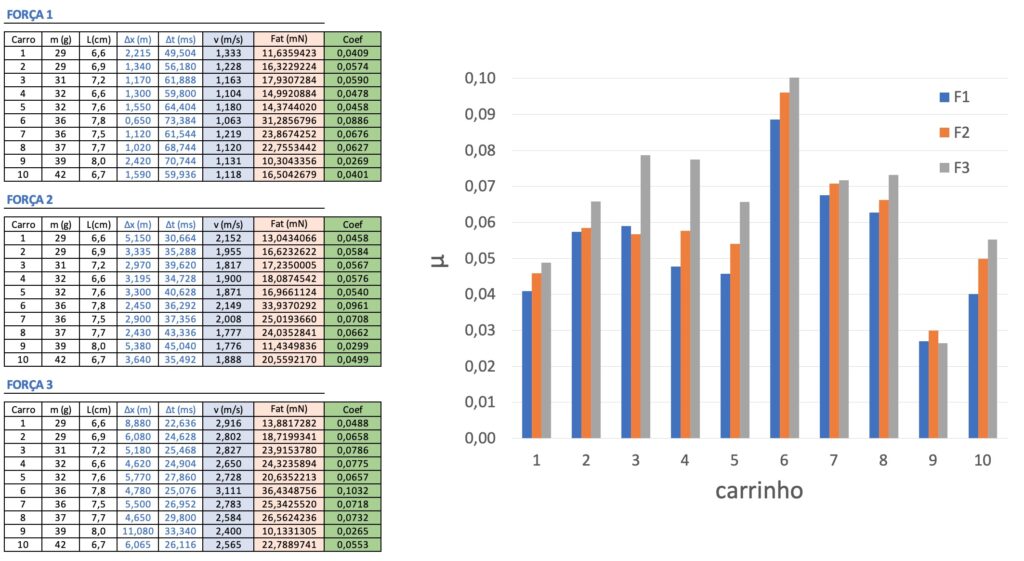
O melhor modo de analisar os resultados é utilizando um tipo de gráfico chamado de histograma. No eixo x, estão as categorias (no nosso caso, cada carro), e o eixo y estão os dados medidos do coeficiente de atrito. Cada cor indica um nível de força.
O primeiro detalhe que chama atenção é que, na maioria dos casos, o coeficiente de atrito depende da força de lançamento de modo que quanto maior a força maior o valor de $\mu$. Mas note também que, na maioria dos casos, os valores de $\mu$ não aumentam muito em relação à força. Por exemplo, para o carro 1, $\mu$ varia de 0,0409 para 0,0488 entre F1 e F3. Note também que $\Delta x$ cresce de 2,215 m para 8,880 m. Ou seja, o carrinho viaja uma distância quase 4 vezes maior. Devido a distância maior, o carrinho também passa por muito mais junções e pista e está sujeito a bater nas laterais da pista quando lançado com F3 em comparação com F1. E estas junções e choques com as bordas certamente afetam a medida do coeficiente de atrito. De qualquer forma, considero as variações pequenas, e estou convencido de que o coeficiente de atrito do carrinho 1 é aproximadamente a média de F1 a F3. No caso do carrinho 1, algo em torno de 0,045.
Uma visão geral mostra que os coeficientes de atrito varia muito entre os modelos. De certa forma, isto explica porque nem todos os carrinhos conseguiram completar o loop quando soltos da mesma altura no post sobre a Física do loop. Se você já brincou ou observou crianças brincando com os carrinhos, certamente sabe que parte da diversão é descobrir quais carrinhos irão completar uma pista construída (veja este vídeo para um exemplo que as crianças adoram).
Com este experimento, tive algumas surpresas interessantes. Sempre usei o carrinho 7 em vários experimentos aqui no blog por achar que ele era mais veloz que o carrinho 1, mas me enganei redondamente. Mas minha maior surpresa foi descobrir que o carrinho 9, feito para levar uma câmera Go Pro Sessions (nem o carrinho e nem a câmera são mais fabricados), é o mais eficiente de todos. Seu coeficiente de atrito é de cerca de 0,025 quando o segundo melhor carrinho (o carro 1) tem praticamente O DOBRO do coeficiente de atrito. Imagino que isto seja feito de propósito, pois o carrinho precisa levar a câmera nas costas para executar percursos e fazer vídeos irados como este aqui.
Para concluir, lembro a vocês que atrito é um assunto que rende bastante material, e ainda estou devendo a conclusão da sequência de posts sobre atrito com um experimento provando que $F_{at}=\mu N$ em pistas inclinadas, e consequentemente, em qualquer situação.