Conservação da energia mecânica com Hotwheels e Arduino

O nosso sensor de passagem para medir velocidade continua rendendo várias experiências interessantes e divertidas. No posto de hoje vamos falar sobre conservação de energia mecânica utilizando novamente uma pista de carrinhos Hotwheels e um sensor de velocidade.

Tipos de energia mecânica

Energia mecânica é todo tipo de energia associada ao movimento e/ou posição dos corpos. Na escola a gente aprende que há dois tipos de energia mecânica:

• Energia cinética: um tipo de energia que está associada ao movimento dos corpos. Se um corpo de massa $m$ se move com velocidade $v$, este corpor possui uma energia cinética $E_C$ dada por:

$$E_C = \frac{m v^2}{2}$$

• Energia potencial: um tipo de energia que está associado a posição de um objeto em relação a algum tipo de campo de força que interaja com o objeto. Na escola, a gente aprende que há 3 tipos de energia potencial: energia potencial gravitacional, energia potencial elástica, e energia potencial elétrica. Em outras oportunidades iremos discutir mais especificamente as diferentes formas de energia potencial, mas neste post iremos focar apenas na energia potencial gravitacional. Sabemos que qualquer objeto ou ser vivo em nosso planeta está sujeito ao campo gravitacional da Terra. Se elevarmos e soltarmos um objeto de massa $m$ a uma altura $H$ do solo, sabe-se que este objeto vai cair. E quanto mais alta for a altura $H$, maior vai ser a velocidade com que o objeto atinge o solo. Antes de o objeto adquirir energia cinética devido ao movimento de queda, o objeto ganhou energia potencial gravitacional dada por:

$$U_g = m g H$$

Conservação da energia mecânica

Um princípios mais importantes que regem tudo o que existe no universo é o da conservação da energia, seja ela mecânica ou não-mecânica. Quando não há forças que dissipem energia, toda a energia mecânica é conservada. Vejamos os exemplos dados na Figura 1.

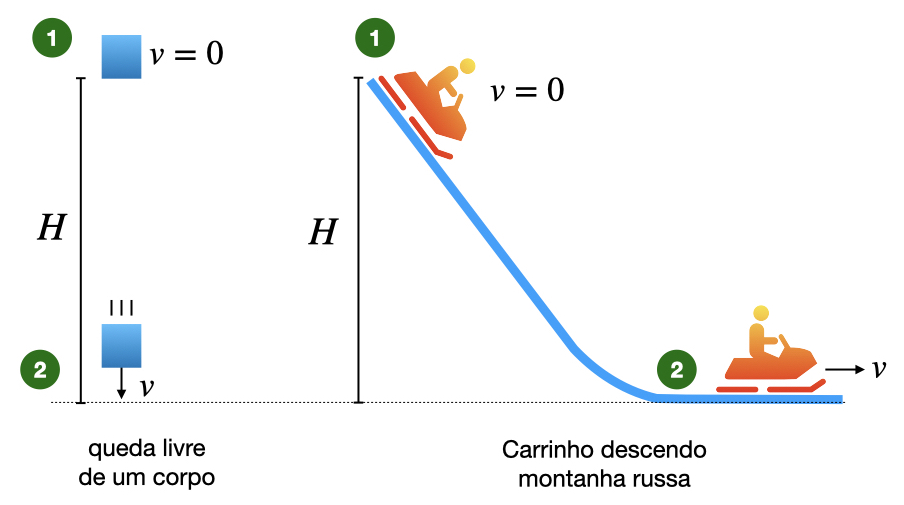
A Figura 1 mostra dois casos: a queda livre a esquerda, e de um carrinho descendo uma montanha russa. Nos dois casos, o corpo está parado e a uma altura $H$ em relação ao solo. A energia mecânica total do corpo no ponto 1 é:

$$E_{M,1} = E_{C,1} + U_{g,1} = 0 + m g H = m g H.$$

Como o corpo está parado no ponto 1, sua velocidade é nula ($v_1 = 0$), portanto, sua energia cinética também é zero ($E_{C,1}=0$). No ponto 2, o objeto está a uma altura zero em relação ao solo, e se movendo com uma velocidade $v_2$ que desconhecemos. Portanto, sua energia mecânica total é dada por:

$$E_{M,2} = E_{C,2} + U_{g,2} = \frac{m v_2^2}{2} + 0 = \frac{m v_2^2}{2}.$$

Se não houver nenhum tipo de força que dissipe energia mecânica (força de atrito com o ar e/ou com o trilho, por exemplo), a energia mecânica total do sistema será conservada, ou seja, será a mesma para os pontos 1 e 2 ($E_{M,1}=E_{M,2}$). Se soubermos a altura $H$ inicial, podemos tirar proveito da conservação da energia mecânica e determinar a velocidade no ponto 2:

$$m g H = \frac{m v_2^2}{2} ~~ \rightarrow ~~ v_2^2 = 2 g H$$

O mais surpreendente desse resultado é que ele independe da massa $m$ do objeto, e também do caminho total percorrido pelo objeto. Note que na queda livre, o corpo percorre apenas uma distância $H$, que é altura de onde o corpo cai. No caso da montanha russa, o carrinho percorre o comprimento $L$ entre os pontos 1 e 2 da pista, que é maior que a altura inicial $H$. Isto só acontece porque o campo gravitacional é dito conservativo (ou seja, conserva energia mecânica), e o que interessa de fato são apenas as posições inicial e final do objeto em relação a superfície da Terra, e não o caminho percorrido.

E se houver forças dissipativas?

Se, em qualquer uma das situações mostradas na Figura 1, houver forças que dissipem a energia mecânica do sistema como a força de resistência do ar e/ou força de atrito com o trilho da montanha russa, a energia mecânica total não será conservada. Neste caso, teremos $E_{M,1} \neq E_{M,2}$. Mas é interessante saber o que ocorre com a diferença de energia mecânica entre os pontos 1 e 2:

$$ \Delta E_M = (E_{C,2}+U_{g,2})- (E_{C,1}+U_{g,1}) = \Delta E_C + \Delta U_g $$

A equação acima mostra que a variação de energia mecânica é simplesmente a soma das variações de todos os tipos de energia mecânica. No nosso caso específico da Figura 1, temos que

$$ \Delta E_M = \frac{m v_2^2}{2}~-~m g H.$$

Agora pensemos o seguinte, se houver qualquer tipo de atrito (com o ar e/ou trilho), a velocidade no ponto 2 será menor que na situação em que não há atrito. Portanto, obteremos $\Delta E_M < 0$ sempre !!!! Por outro lado, se $\Delta E_M >0$, é porque a velocidade do corpo no ponto 2 é maior do que quer deveria ser na situação em que não há atrito. E isso só pode ocorrer com uma única condição, houve alguma forma de energia dada ao corpo que serviu de propulsão para ganho de velocidade !!!

O experimento

Para estudar a conservação da energia mecânica, vamos utilizar o experimento mostrado na Figura 2, onde simulamos um trecho de queda de uma montanha russa. Vamos soltar dois carrinhos (de massas diferentes) de várias alturas diferentes, e medir sua velocidade na parte horizontal da pista.

Se houver conservação de energia mecânica no nosso experimento, sabe-se que $v_1^2 = 2 g H$, então o gráfico $v_1^2$ vs $H$ construído com os dados de cada lançamento deve ser uma linha reta cujo coeficiente linear é igual a $2 g$, independente portanto da massa do carrinho. Se os dados experimentais ficarem abaixo desse gráfico, é porque há algum tipo de atrito no nosso experimento. Se ficarem acima, é porque há algum tipo de propulsão sendo dada aos carrinho, conforme mostrado na Figura 3.

Medidas

A Figura 4 mostra a tabela dos dados medidos para dois carrinhos diferentes (os mesmos do post anterior sobre a física do lançamento oblíquo). Ao todo foram realizados 10 lançamentos variando entre uma altura mínima de 25,5 cm e uma altura máxima de 57,5 cm.

É interessante notar que os dados dos dois carrinhos são idênticos, apesar das massas e tamanhos diferentes, e apresentando os valores de $v^2$ ligeiramente abaixo da linha teórica de conservação de energia. Para o lançamento de $H$ = 57,5 cm, a perda de energia é de menos de 1%, já para $H$ = 25,5 cm, a perda de energia é de cerca de 13%. No nosso sistema há três mecanismos principais de dissipação de energia: atrito nos pneus dos carrinhos, atrito com a pista, e a resistência do ar. Em princípio, é basta difícil separar a contribuição de cada um destes efeitos sem a montagem de experimentos mais sofisticados.

É importante também mencionar que há outra contribuição de energia mecânica que não foi considerada no problema: a energia cinética associada a rotação dos pneus. Embora este efeito seja bem complicado de explicar sem um experimento mais detalhado, acredito que esta contribuição é muito pequena devido ao pequeno diâmetro dos pneus, e tem pouco impacto nos resultados.

Apesar do pequeno efeito de dissipação de energia mecânica, concluo que, em uma primeira aproximação, podemos considerar que a energia mecânica foi conservada neste experimento.

Assista aqui demonstração deste experimento em vídeo:

Observação sobre a medida da velocidade

Neste experimento, a velocidade foi medida usando o sensor de passagem descrito aqui, mas com uma pequena modificação. Como foram feitas muitas medidas em alturas muito próximas umas das outras, foi necessário mudar o código do Arduino para que ele medisse os tempos de passagem com precisão de microssegundos. Utilizamos o mesmo código descrito aqui, mas trocando a chamada da função millis() pela função micros(). Segue abaixo o código utilizado para medir tempos de passagem com precisão de microssegundos.

// Definição das entradas

// define o pino digital 3 como entrada do fototransistor
const int FOTOpin = 3; 
bool ligado = false;
long dt;

void setup() {
 // coloque aqui o código de inicialização que será executada apenas uma vez.
  
  // configuração do pino 3 como entrada
  pinMode(FOTOpin, INPUT); 

  // inicializa a saída serial do Arduino
  Serial.begin(9600); 
 
}

void loop() {
  // put your main code here, to run repeatedly:

  // leitura do fotodiodo
  int v1 = digitalRead(FOTOpin); 

  // detecta se um objeto chegou no sensor
  if ((v1 == HIGH) & (ligado == false)){
    ligado = true;
    dt = micros();
  }  

  // detecta se um objeto saiu do sensor
  if ((v1 == LOW) & (ligado == true)){
    ligado = false;
    dt = micros() - dt;
    Serial.print("Tempo de passagem (micro seg.) = ");
    Serial.println(dt);
  }  

}